NB I was careless about naming row and column, and some of the indexing is dodgy. This needs sorting before trying inverse matrix. At present the functions work correctly I believe.
*************************************************
If one of the dimensions has value one, we refer to the special cases of row and column vectors. A row or column vector with two elements might represent position on a screen, and one with three elements can represent position in 3-space. Matrices can be added and subtracted and multiplied. They can be transposed, and 'inverted', which gives an easy way to solve linear equations. You need to be aware that the order of operations matters with matrix operations- they may not 'be commutable'. Matrices find applications in most scientific fields. In physics, matrices are used to study electrical circuits, optics, and quantum mechanics. See Wikipedia.
Through the years I have regularly programmed matrix operations, usually using 2D arrays. This works fine, but gives no easy way to handle the matrix as an entity- you can't refer to it as a whole, just via its aray elements. This means entering, saving or manipulating matrices is clumsy. You have to handle each element separately. Re-using the code in a different context tends to be harder than re-writing from scratch. On occasion I've made routines for matrices of 2 columns by 2 rows ( eg for operations on screen coordinates when scaling, shearing or translating), and of other sizes in various cases. For linear equation solving we want much bigger matrices. Gauss Jordan matrix inversion for example was written from scratch. It would be interesting to be able to write such programs with a common library.
In Liberty BASIC you have to pre-dimension 2D arrays, and this either leaves empty entries for small matrices, or an un-desirable limit when you might want to enter arbitrarily big matrices.
One of the Rosetta Code tasks asked for matrix operations on an array of ANY size, which spurred me to write some routines. It turned into a fun programming exercise, not yet completed. Ideally I'd like to make matrix operators which accept and return 'complex' elements....
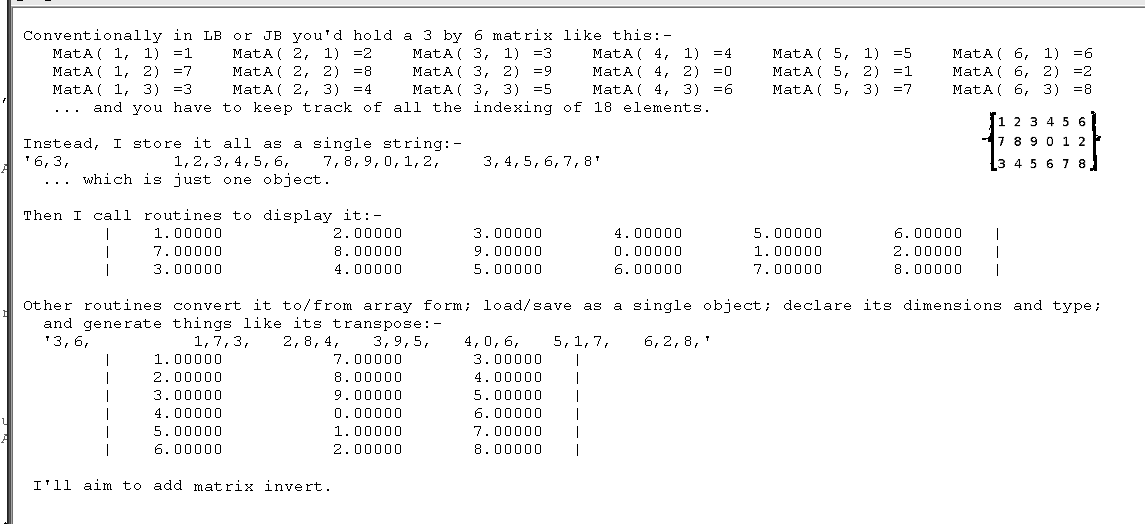
One of the strengths of other languages can be to either have pre-defined matrix operations, or allow their creation as custom-designed structures. In LB you can do something similar by creating a way of storing all the required information in a string, and then write functions that operate on that string as a single entity.
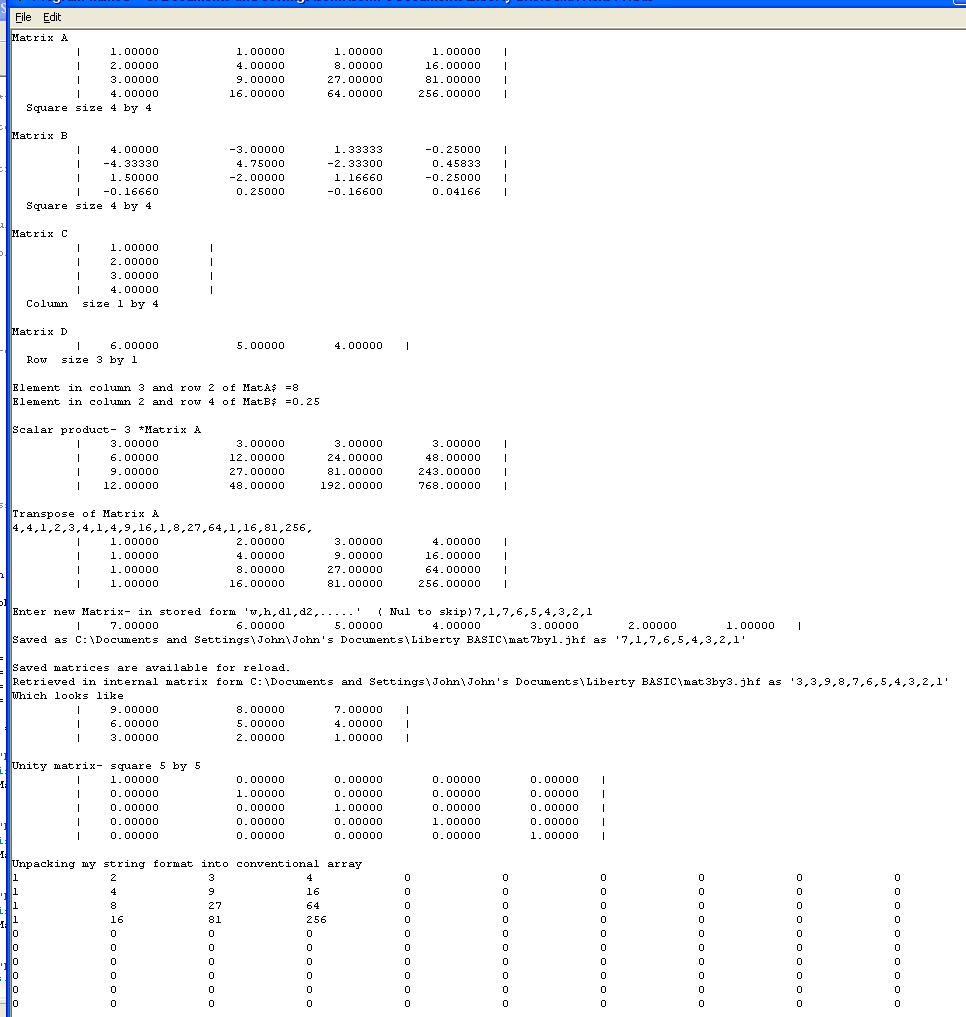
All you need to do is copy the functions and paste them to the end of your program. You also need to add 'dim GlobalArray( 100, 100)' near the beginning, to enable the scratchpad array for feeding array data in and out of calling programs. You now can create, save, scalar multiply, matrix multiply and find determinants, and display them easily.
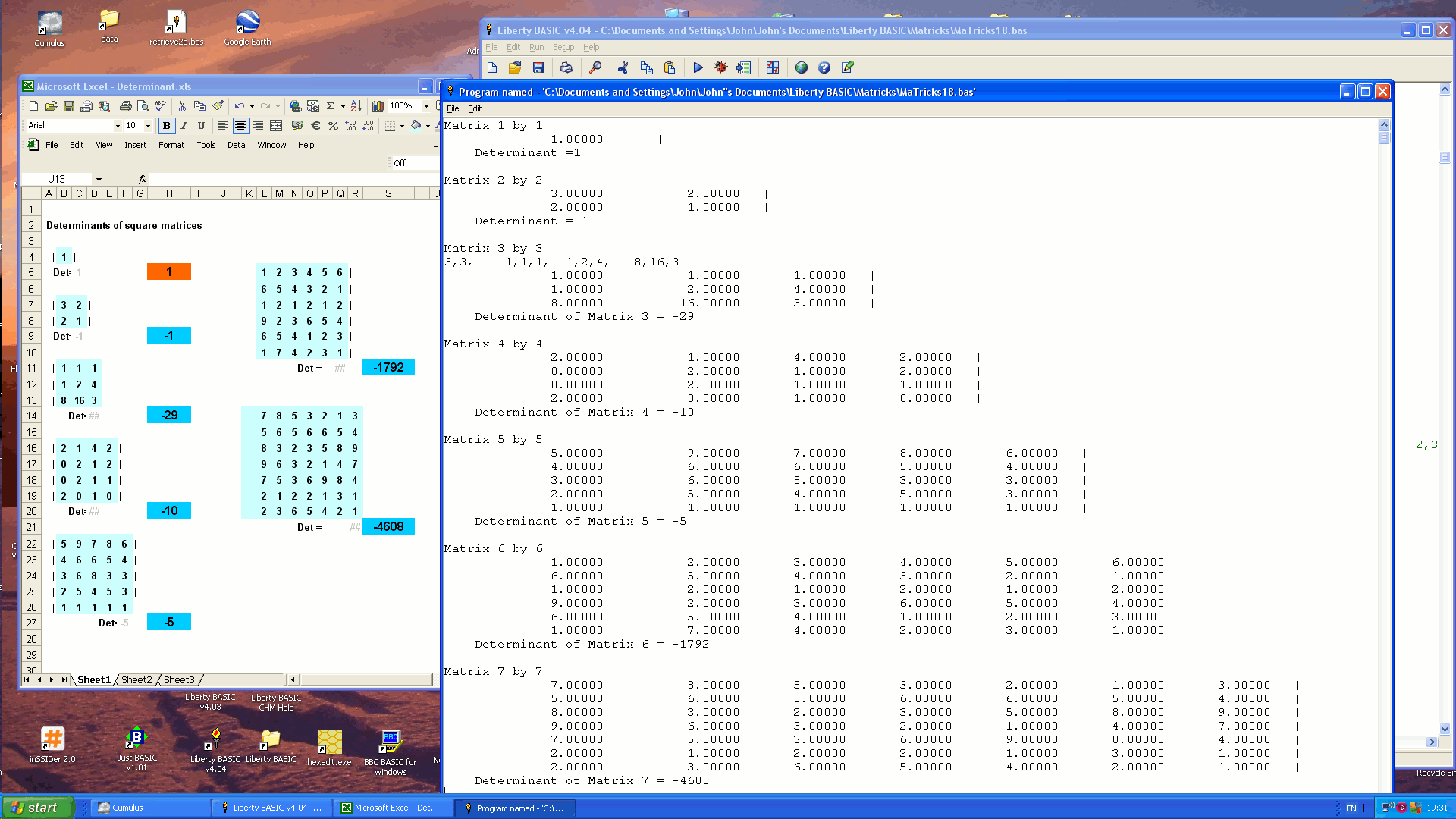
HOWEVER you are warned that the determinant, which takes times depending on (matrix-dimension)!, already takes up to a minute on a seven-by-seven matrix. For anything larger I recommend using a spreadsheet's matrix functions, or a compiled language. My aim was to get easy handling from within LB, and that I now have.
A nice side-effect of programming like this was that I could use 'eval' on the matrix string, so you can enter an element as '0.3333', but also as '1/3'.
Demonstration of agreement with Excel/ Libre Office.
