Complex number calculations
One thing missing in many languages, including LB/JB, is a way to represent and operate on complex numbers. 'Typing' of variables, and how they can (self)-convert) is an important part of specifying a language. I like having integers, floats, strings, binary, boolean, and custom designed variables. But can manage with fewer!
Even Fortran had a complex-variable type a long time ago! So... what to do when we want to use them? There are two basic types of work-around. One is two use two separate variables for each, to hold the real and 'imaginary' part. This makes housekeeping and programming harder to do and read. Or hold them within a single string variable in some simple format. ( tsh too seems to have gone for this approach) In addition, you really want to package the calculations to make them become callable functions or procedures so you can then write your Mandelbrot or whatever.
You also have to use a variation of the atn function, called atan2, which gives correct angle results in all four quadrants.
Forum searches will turn up excellent contributions from tsh, steelweaver and others.
The following is a ( at present unfinished) project to make a graphic-displaying, complex-number calculator, using both the ( a +ib) and ( r, theta) polar notations. It is designed to be self-documanting, rather than for concise efficiency. (ie it 'just grew', and should really be re-written now I know what can be done. I'd love to receive helpful suggestions!
Follow up posts at LB Conforum and LB Community Wiki.
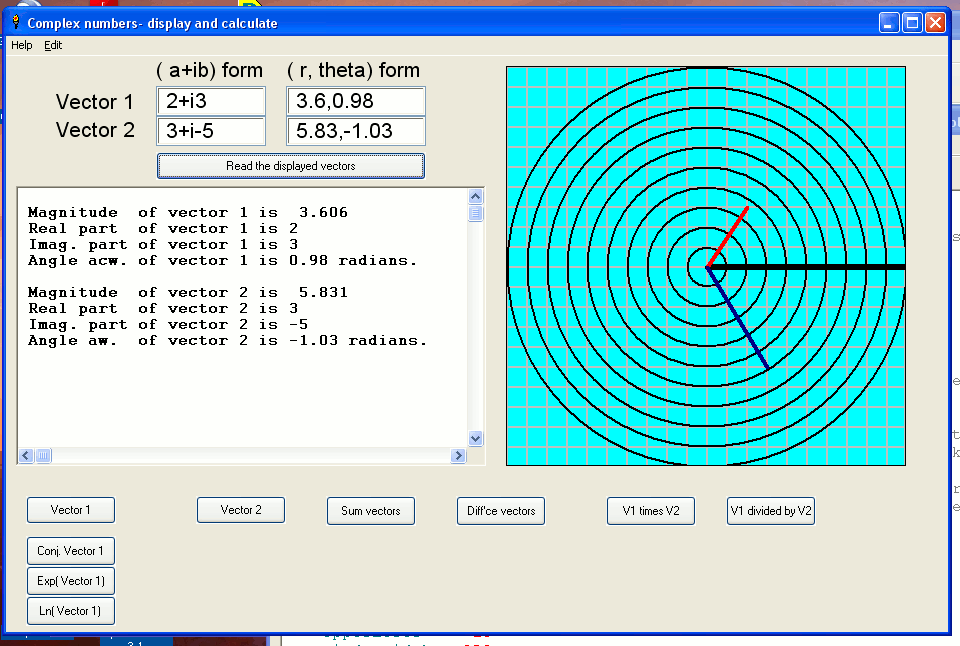
' Complexity3.bas - display of one or two vectors, and various complex functions
' To-do's
' Check all results
' Enable editing of ( r,theta) form to work.
' Correct all displays to "##.##".
' error trap for eg division where both =0
' Add graphic printout
' Show V1 & V2 along with sum, difference, product, quotient
' Show V1 along with conj. V1, cexp and cln.
' Add ability to rotate V1 by chosen angle
' Add a routine to use mouse to create V1 &/or V2 rather than textboxes
' Add [AboutComplexNumbers] file and link to http://en.wikipedia.org/wiki/Complex_number
' Add [Usage] section
' Add scale factor up/down *2 buttons, and superpose x/y/r min/max
' Add ln/exp possibly. NB Multiple values of roots, etc, eg 1^(1/3)
' Add r theta display of v1 and v2 Done 01/06/10
' If v2 empty, disable ops needing two vectors
nomainwin
UpperLeftX = 10
UpperLeftY = 10
WindowWidth =950
WindowHeight =630
menu #w, "Help", "About complex numbers", [AboutComplexNums], "Using this program", [Usage]
statictext #w.st1, "Vector 1", 50, 34, 80, 30
statictext #w.st2, "Vector 2", 50, 62, 80, 30
statictext #w.st3, "( a+ib) form ( r, theta) form", 150, 2, 300, 26
textbox #w.tb1, 150, 30, 110, 30
textbox #w.tb2, 150, 60, 110, 30
textbox #w.tb3, 280, 30, 140, 30
textbox #w.tb4, 280, 60, 140, 30
texteditor #w.te, 10, 130, 470, 280
graphicbox #w.g1, 500, 10, 400, 400
button #w.b1, "Read the displayed vectors", [ReadVectors], UL, 150, 96
button #w.b2, "Vector 1", [DisplayV1], UL, 20, 440
button #w.b3, "Vector 2", [DisplayV2], UL, 190, 440
button #w.b4, "Conj. Vector 1", [ConjV1], UL, 20, 480, 90, 30
button #w.b9, "Exp( Vector 1)", [ExpV1], UL, 20, 510, 90, 30
button #w.b10,"Ln( Vector 1) ", [LnV1], UL, 20, 540, 90, 30
button #w.b5, "Sum vectors", [V1PlusV2], UL, 320, 440, 90, 30
button #w.b6, "Diff'ce vectors", [V1MinusV2], UL, 450, 440, 90, 30
button #w.b7, "V1 times V2", [V1TimesV2], UL, 600, 440, 90, 30
button #w.b8, "V1 divided by V2", [V1DivV2], UL, 720, 440, 90, 30
open "Complex numbers- display and calculate" for window as #w
#w, "trapclose [quit]"
#w.g1, "when leftButtonMove [paint]"
#w.te, "!font courier 14 bold"
#w.st1, "!font arial 16"
#w.st2, "!font arial 16"
#w.st3, "!font arial 16"
#w.tb1, "!font arial 16"
#w.tb2, "!font arial 16"
#w.tb3, "!font arial 16"
#w.tb4, "!font arial 16"
#w.tb1, "2+i3"
#w.tb2, "3+i-5"
#w.tb3, "3.6,0.98"
#w.tb4, "5.83,-1.03"
#w.b2, "!disable"
#w.b3, "!disable"
#w.b4, "!disable"
#w.b5, "!disable"
#w.b6, "!disable"
#w.b7, "!disable"
#w.b8, "!disable"
#w.b9, "!disable"
#w.b10,"!disable"
gosub [axes]
wait
[paint]
#w.g1, "set "; MouseX; " "; MouseY ' This will become routine to drag to new end-point...
wait
[ReadVectors]
#w.g1, "drawbmp display 0 0"
#w.tb1, "!contents? a$";
#w.tb2, "!contents? b$";
#w.te, ""
#w.te, " Magnitude of vector 1 is "; mag$( a$)
#w.te, " Real part of vector 1 is "; real( a$)
#w.te, " Imag. part of vector 1 is "; imag( a$)
#w.te, " Angle acw. of vector 1 is "; theta( a$); " radians."
#w.te, ""
#w.te, " Magnitude of vector 2 is "; mag$( b$)
#w.te, " Real part of vector 2 is "; real( b$)
#w.te, " Imag. part of vector 2 is "; imag( b$)
#w.te, " Angle aw. of vector 2 is "; theta( b$); " radians."
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( a$); " "; 200 -20 *imag( a$); " ; up"
#w.g1, " goto 200 200 ; color darkblue ; down ; goto "; 200 +20 *real( b$); " "; 200 -20 *imag( b$); " ; up"
#w.b2, "!enable"
#w.b3, "!enable"
#w.b4, "!enable"
#w.b5, "!enable"
#w.b6, "!enable"
#w.b7, "!enable"
#w.b8, "!enable"
#w.b9, "!enable"
#w.b10,"!enable"
wait
[DisplayV1]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Vector 1 only"
#w.te, " Vector 1 equals "; a$
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( a$); " "; 200 -20 *imag( a$); " ; up"
wait
[DisplayV2]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Vector 2 only"
#w.te, " Vector 2 equals "; b$
#w.g1, " goto 200 200 ; color darkblue ; down ; goto "; 200 +20 *real( b$); " "; 200 -20 *imag( b$); " ; up"
wait
[ConjV1]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Conjugate of vector 1"
#w.te, " Conj. "; a$; " equals "; using( "##.##", real( conj$( a$))); "+i"; using( "##.##", imag( conj$( a$)))
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( a$); " "; 200 +20 *imag( a$); " ; up"
wait
[ExpV1]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Exp( vector 1)"
#w.te, " Exp( "; a$; ") equals "; using( "##.##", real( cexp$( a$))); "+i"; using( "##.##", imag( cexp$( a$)))
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( cexp$( a$)); " "; 200 +20 *imag( cexp$(a$)); " ; up"
wait
[LnV1]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Ln( vector 1)"
#w.te, " Ln( "; a$; ") equals "; using( "##.##", real( cln$( a$))); "+i"; using( "##.##", imag( cln$( a$)))
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( cln$( a$)); " "; 200 +20 *imag( cln$(a$)); " ; up"
wait
[V1PlusV2]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Sum of vectors 1 and 2"
#w.te, " "; a$; " plus "; b$; " equals "; real
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( cadd$( a$, b$)); " "; 200 +20 *imag( cadd$( a$, b$)); " ; up"
wait
[V1MinusV2]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Vector 1 minus vector 2"
#w.te, " "; a$; " minus "; b$; " equals "; csub$( a$, b$)
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( csub$( a$, b$)); " "; 200 +20 *imag( csub$( a$, b$)); " ; up"
wait
[V1TimesV2]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Product of vector 1 and 2"
#w.te, " "; a$; " times "; b$; " equals "; cmul$( a$, b$)
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( cmul$( a$, b$)); " "; 200 +20 *imag( cmul$( a$, b$)); " ; up"
wait
[V1DivV2]
#w.g1, "drawbmp display 0 0"
#w.te, "!cls"
#w.te, " Vector 1 divided by vector 2"
#w.te, " "; a$; " div'd by "; b$; " equals "; cdiv$( a$, b$)
#w.g1, "size 4 ; goto 200 200 ; color red ; down ; goto "; 200 +20 *real( cdiv$( a$, b$)); " "; 200 +20 *imag( cdiv$( a$, b$)); " ; up"
wait
[quit]
close #w
end
[axes]
#w.g1, "color lightgray ; down ; size 2 ; fill cyan"
for y =-10 to 10
#w.g1, "up ; goto 0 "; 200 +y *20; " 0 ; down ; goto 400 "; 200 +y *20
next y
for x =-10 to 10
#w.g1, "up ; goto "; 200 +x *20; " 0 ; down ; goto "; 200 +x *20; " 400"
next x
#w.g1, "size 6 ; goto 400 200 ; down ; color black ; goto 200 200 ; size 2"
for radius =1 to 10
#w.g1, " circle "; radius *20
next radius
#w.g1, "getbmp display 0 0 400 400"
bmpsave "display", "display.bmp"
return
' Use atan2 so angles are not ambiguous
function atan2( y, x)
if x >0 then at =atn( y /x)
if y >=0 and x <0 then at =atn( y /x) +pi
if y <0 and x <0 then at =atn( y /x) -pi
if y >0 and x =0 then at = pi /2
if y <0 and x =0 then at = 0 -pi /2
if y =0 and x =0 then notice "undefined": end
atan2 =at
end function
' ___________ functions of one complex number __________________
function real( c$) ' Separate out the real value
p =instr( c$, "+")
r =val( left$( c$, p -1))
real =r
end function
function imag( c$) ' and the complex one.
p =instr( c$, "+")
i =val( mid$( c$, p +2))
imag =i
end function
function theta( c$) ' Find acw angle to the vector.
p =instr( c$, "+")
r =val( left$( c$, p -1))
i =val( mid$( c$, p +2))
theta =atan2( i, r)
theta =0.01 *int( 100 *theta)
end function
function conj$( c$) ' Conjugate of a+ib is a-ib.
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
conj$ =str$( realc) +"+i" +str$( -1 *imagc)
end function
function mag$( c$) ' Magnitude is the length of the vector
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
mag =( realc^2 +imagc^2)^0.5
mag$ =using( "##.###", mag)
end function
function cexp$( c$) ' exp( a +ib) =exp( a) *exp( ib) ?????
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
cexp$ =str$( exp( realc) *cos( imagc)) +"+i" +str$( exp( realc) *sin( imagc))
end function
function cln$( c$) ' ???????
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
cln$ =""
end function
' _____________________ functions of two complex numbers ___________________________________
function cmul$( c$, d$)
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
p =instr( d$, "+")
reald =val( left$( d$, p -1))
imagd =val( mid$( d$, p +2))
cmul$ =str$( realc *reald -imagc *imagd) +"+i" +str$( 2 *imagc +imagd)
end function
function cdiv$( c$, d$)
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
p =instr( d$, "+")
reald =val( left$( d$, p -1))
imagd =val( mid$( d$, p +2))
q =reald^2 +imagd^2
rp =( realc *reald +imagc *imagd) /q
ip =( imagc *reald -realc *imagd) /q
cdiv$ =str$( rp) +"+i" +str$( ip)
end function
function cadd$( c$, d$)
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
p =instr( d$, "+")
reald =val( left$( d$, p -1))
imagd =val( mid$( d$, p +2))
cadd$ =str$( realc +reald) +"+i" +str$( imagc +imagd)
end function
function csub$( c$, d$)
p =instr( c$, "+")
realc =val( left$( c$, p -1))
imagc =val( mid$( c$, p +2))
p =instr( d$, "+")
reald =val( left$( d$, p -1))
imagd =val( mid$( d$, p +2))
csub$ =str$( realc -reald) +"+i" +str$( imagc -imagd)
end function
e-mail me.
