Turtle variation- controlled by path curvature


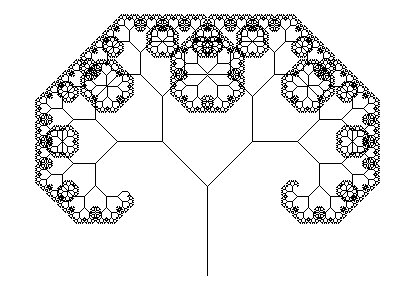
It's heading for a half century since Seymour Papert introduced LOGO, a computer language designed to modify and improve logical problem tackling with young students. BYTE magazine devoted a special edition to the language- picture above is part of the cover.
The aspect that really caught on was the ability to control a 'turtle'- whether on screen or actual hardware- and write procedures that created beautiful or unusual geometric shapes. Just use commands to move forward,to turn, and to raise/lower a'pen'. There was an emphasis on experimenting- if something didn't work right, learn to investigate WHY but meanwhile enjoy a novel result!
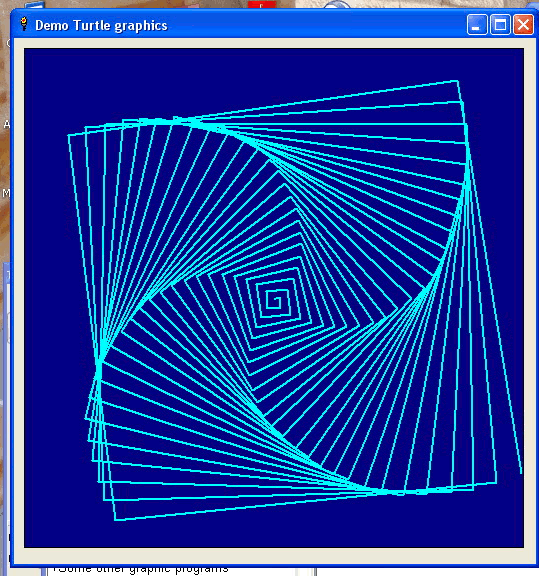
There's one slight problem. Displays are based on an integer x/y grid. Fine if you move only integer amounts and on the x or y axis. But move non-integral distances, or even integral distances along an arbitrary path angle, and you end at a non-integral location that will be represented by the nearest integral location. If the location is internally stored as a float, there's no problem. But LB stores the present location as the nearest integer pair, and this means errorscan accumulate in multiple iterative calls.

This is easily solved by replacing LB's native commands with simple procedures that store location and angle as floats. ( Again, see the linked pages)
This allows accurate plotting of deep recursive graphics. An earl example was..
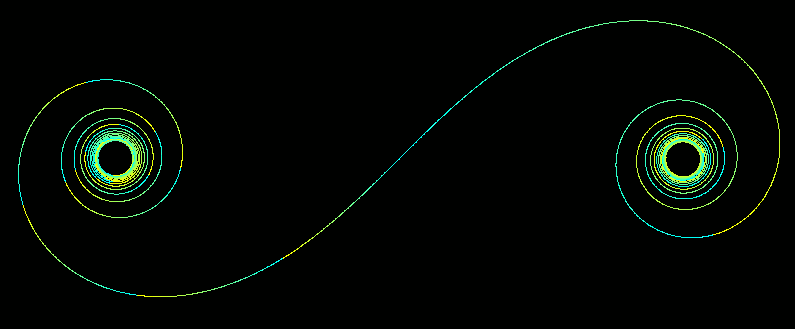
Recently I remembered I'd always wanted to plot Cornu spirals and been put off by their definition in terms of complex integrals. But it turns out that by using a turtle that move incrementally making slightly sharper turns every step achieves the desired curve!
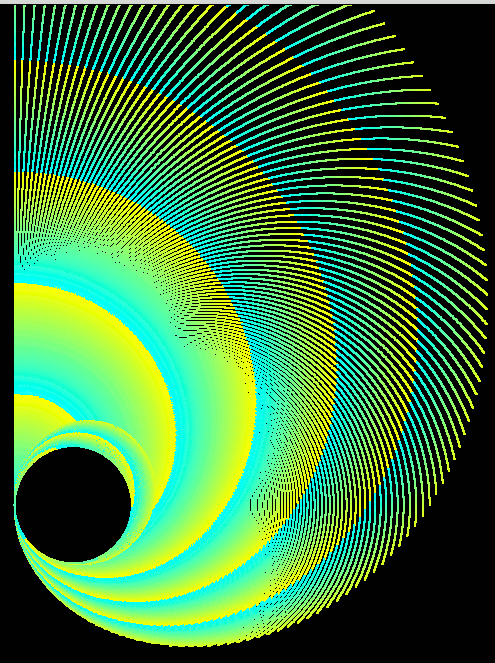
First I checked that turning the SAME amount at each tiny increment correctly produces circles...
. . . and then implemented the steadily increasing curvature...
I also played with curves where the curvature increases at an increasing rate- producing what have been called 'curlicues'.

' Circles.
' This is the trail left by a turtle which
' takes steps of a fixed size and turns rightt
' the same amount each step.
' ie d( curvature) /dt =k
' NB LB's turtle accepts only integer steps and angles.
' So here I use my own turtle routines.
nomainwin
WindowWidth =950
WindowHeight =750
open "Curlicues" for graphics_nsb as #wg
#wg "trapclose quit"
#wg "down ; fill black ; flush ; size 1"
global pi, TX, TY, Ttheta
pi =4 *atn( 1): TX =252: TY =500: Ttheta =270
' turtle starts at TX, TY, pointing North
f = 0.1 ' angle turned at each iteration
st = 0.1 +rnd( 1) ' step size per iteration
for f = 0 to 2.5 step 0.005
TX =252: TY =500: Ttheta =270
for i =0 to 1.5e3
call turn f
#wg "color "; str$( int( f *3000) mod 255); " 255 "; str$( 255 -int( f *5000) mod 255)
call forward st
'if i mod 2e3 =0 then ' to save for an animated GIF.
' #wg "flush"
' #wg "getbmp scr 0 0 960 710"
' bmpsave "scr", "bmp/scrJ" +str$( time$( "seconds")) +".bmp"
' #wg "cls ; drawbmp scr 0 0"
'end if
scan
next i
next f
#wg "flush"
wait
sub turn angle ' increment/update global turtle direction ( in DEGREES)
Ttheta =( Ttheta +angle) 'mod 360
end sub
sub forward s
dx =s *cosRad( Ttheta)
dy =s *sinRad( Ttheta)
#wg "down ; line "; TX; " "; TY; " "; TX +dx; " "; TY +dy; " ; up"
TX =TX +dx
TY =TY +dy
end sub
function sinRad( a)
sinRad =sin( a *pi /180)
end function
function cosRad( a)
cosRad =cos( a *pi /180)
end function
function co$( I)
r =int( 128 +127 *sin( I / 330000))
g =int( 128 +127 *sin( I / 170000))
b =int( 128 +127 *sin( I / 070000))
co$ =str$( r) +" " +str$( g) +" " +str$( b)
end function
sub quit h$
close #h$
end
end sub
' Cornu spiral.
' This is the trail left by a turtle which
' takes steps of a fixed size and turns right
' a linearly increasing amount each step.
' ie d( curvature) /dt =k *t
' Related to clothoid /Cornu curves/spiral.
' and also the shape of a pig's tail...
' A Euler spiral is a curve whose curvature changes
' linearly with its curve length (the curvature of
' a circular curve is equal to the reciprocal of the radius).
' NB LB's turtle accepts only integer steps and angles.
' So here I use my own turtle routines.
nomainwin
WindowWidth =950
WindowHeight =750
open "Curlicues" for graphics_nsb as #wg
#wg "trapclose quit"
#wg "down ; fill black ; flush ; size 1"
global pi, TX, TY, Ttheta
pi =4 *atn( 1): TX =252: TY =500: Ttheta =315
' turtle starts at TX, TY, pointing North
f = 0.0005 ' angle turned at each iteration
st = 0.6 ' step size per iteration
TX =452: TY =350: Ttheta =315
for i =0 to 5e3
call turn f
f =f +0.4e-3
#wg "color "; str$( int( ( i mod 1024) /4)); " 255 "; str$( 255 -int( ( i mod 1024) /4))
call forward st
scan
next i
TX =452: TY =350: Ttheta = 135
f = 0.001
for i =0 to 5e3
call turn f
f =f +0.4e-3
#wg "color "; str$( i mod 256); " 255 "; str$( 255 -( i mod 256)) 'co$( i)
call forward st
scan
next i
#wg "flush"
wait
sub turn angle ' increment/update global turtle direction ( in DEGREES)
Ttheta =( Ttheta +angle) 'mod 360
end sub
sub forward s
dx =s *cosRad( Ttheta)
dy =s *sinRad( Ttheta)
#wg "down ; line "; TX; " "; TY; " "; TX +dx; " "; TY +dy; " ; up"
TX =TX +dx
TY =TY +dy
end sub
function sinRad( a)
sinRad =sin( a *pi /180)
end function
function cosRad( a)
cosRad =cos( a *pi /180)
end function
function co$( I)
r =int( 128 +127 *sin( I / 330000))
g =int( 128 +127 *sin( I / 170000))
b =int( 128 +127 *sin( I / 070000))
co$ =str$( r) +" " +str$( g) +" " +str$( b)
end function
sub quit h$
close #h$
end
end sub
' Curlicue spiral.
' This is the trail left by a turtle which
' takes steps of a fixed size and turns right
' a linearly increasing amount each step.
' ie d( curvature) /dt =k( t) *t
' Related to clothoid /Cornu curves/spiral.
' and also the shape of a pig's tail...
' A Euler spiral is a curve whose curvature changes
' linearly with its curve length (the curvature of
' a circular curve is equal to the reciprocal of the radius).
' NB LB's turtle accepts only integer steps and angles.
' So here I use my own turtle routines.
nomainwin
WindowWidth =950
WindowHeight =750
open "Curlicues" for graphics_nsb as #wg
#wg "trapclose quit"
#wg "down ; fill black ; flush ; size 1"
global pi, TX, TY, Ttheta
pi =4 *atn( 1): TX =252: TY =500: Ttheta =315
' turtle starts at TX, TY, pointing North
' Try
f = 0.0005 ' angle turned at each iteration <<
df = 0.00005 ' amount angle increases by <<
st = 0.8 ' step size per iteration <<
bit = 0.00003 ' increments the increase ( df) each time <<
TX =452: TY =350: Ttheta =315 ' starting position and direction faced.
for i =0 to 5e5
call turn f
f = f +df
df = df +bit
#wg "color "; str$( int( ( i mod 4096) /15)); " 255 "; str$( 255 -int( ( i mod 4096) /16))
call forward st
scan
next i
#wg "flush"
wait
sub turn angle ' increment /update global turtle direction ( in DEGREES)
Ttheta =( Ttheta +angle) 'mod 360
end sub
sub forward s
dx =s *cosRad( Ttheta)
dy =s *sinRad( Ttheta)
#wg "down ; line "; TX; " "; TY; " "; TX +dx; " "; TY +dy; " ; up"
TX =TX +dx
TY =TY +dy
end sub
function sinRad( a)
sinRad =sin( a *pi /180)
end function
function cosRad( a)
cosRad =cos( a *pi /180)
end function
sub quit h$
close #h$
end
end sub