The importance of transition curves
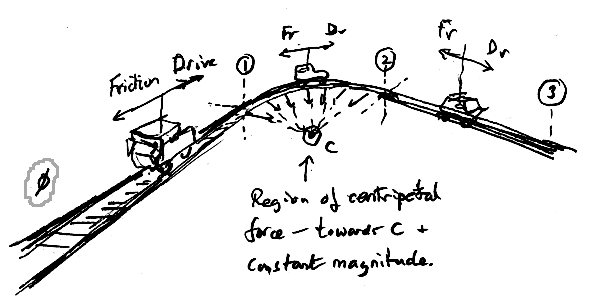

Imagine a car, moving with constant magnitude of velocity, whose path is 0- 1 -2 -3. The friction it experiences from rolling and air are exactly balanced by a motor driving it forward.
Between 1 and 2 it experiences a centripetal force always towards a centre C and again of constant magnitude. It might be provided by rails ( like a train), or friction on wheels, or even a rope!
However, a car ( and its passengers) behaves like a mass on a spring operating in a frictional environment. For it, there is a sudden outward centrifugal force. Applying a sudden force is going to make it head radially outwards to a new equilibrium distance, but it will overshoot. It then returns but not back to the original radius, and the oscillations die away.
In a car, the suspension system of springs and dampers should be set to 'dead beat', ie it will only overshoot slightly and then settle to the new steady position. Worn shock absorbers mean this doesn't happen, and you may get one or more reversals before the steady state.
For a passenger sitting IN the car there is no effective damping, and their body/head will undergo a nomber of oscillations.
When the curve section ends, the return to zero centripetal force makes the same effect in the reverse direction.
Part of the reason many fairground rides are so exciting is that sudden accelerations of your head and the part of the ear that senses motion produce disturbing mental effects, all the way up to violent sickness!
However, more practically important, if you run a train down rails that suddenly go from straight to a fixed radius curve, it will only stay on the rails if they can supply the necessary inward radial force- otherwise it will jump the rails. Or for a car, where the situation is less severe since you 'feed in' a steering deflection smoothly rather than suddenly- but the skid can still happen and you slide off the curved section if friction is not enough.
Engineers solve this disaster situation by feathering the transition from straight to curved with a 'transition curve'. See my earlier post of examples of such curves, Cornu spirals, etc on the LB Board. Much of the code is re-used from there.
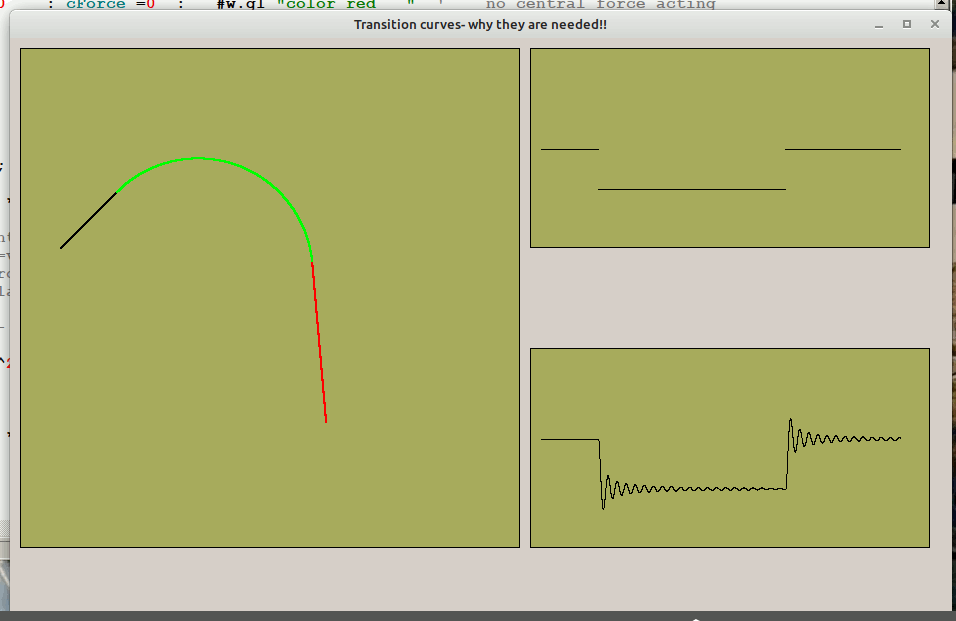
Once you realise that, in the frame of reference of the vehicle the radial motion is independent of the forward motion, so you can work them out independently of each other. Feel free to experiment with any or all of the variables.
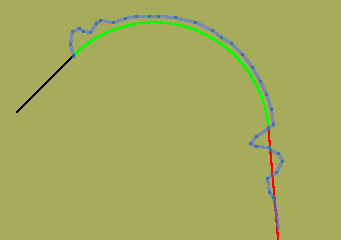 Here I've sketched what your head moves like! I should really add this resultant position to my graphic screens..
Here I've sketched what your head moves like! I should really add this resultant position to my graphic screens..
Note- this is just one of several versions I've played with,,,
' Transition curve- why they are needed!!!
' This is the trail left by a turtle which takes steps of a fixed size.
' Starts at fixed velocity and no acceleration force.
' After 100 steps a force is applied perpendicular to current travel direction.
' so now d( curvature) /dt =k
' NB LB's turtle steps and angles are internally integers. So here I use my own turtle routines.
nomainwin
WindowWidth =950
WindowHeight =600
graphicbox #w.g1 10, 10, 500, 500
graphicbox #w.g2 520, 10, 400, 200
graphicbox #w.g3 520, 310, 400, 200
open "Transition curves- why they are needed!!" for window as #w
#w "trapclose quit"
#w.g1 "down ; size 2 ; fill 170 170 90 ; flush"
#w.g2 "down ; size 1 ; fill 170 170 90 ; flush"
#w.g3 "down ; size 1 ; fill 170 170 90 ; flush"
global pi, TX, TY, Ttheta
pi =4 *atn( 1): TX = 40: TY =200: Ttheta =315
' turtle starts at TX, TY, pointing North
f = 0.0000 ' angle turned at each iteration
st = 0.02 ' step size per iteration
'Initial vehicle conditions
'x = 10 ' initial horizontal position.
't ' initial time.
dt = 0.1 ' time interval between updates.
mass = 1e3 ' mass of moving vehicle.
k = 10
R = 0 ' radius of curved path
'xC =: yC = ' coordinated of centre point.
#w.g1 "down"
for t =0 to 2.5e3 step dt
call turn f
if f =0 and t > 400 then f =0.01 : cForce =1e2: #w.g1 "color green " ' centripetal force acting
if f =0.01 and t >1700 then f =0 : cForce =0 : #w.g1 "color red " ' no central force acting
if R =0 then
R = 80
xC =180
yC =220
end if
call forward st
#w.g1 "line "; TX; " "; TY; " "; TX +dx; " "; TY +dy
#w.g2 "set "; int( 10 +t /2.5e3 *360); " "; 100 +f *4e3
' Can find radial distance and centre from curvature and original angle..
' and from centrifugal force =v^2 /radius.
' Net force towards this centre from .
' force =centriForce -k *displacement radially with k =spring constant.
' Add air drag prop'l v^2.
' if vx >0 then force =force -( vx^2 /100) else force =force +( vx^2 /100)
' print x, vx, accnx
accnx =( cForce -k *x -100 *vx^2 *sgn( vx)) /mass
vx =vx +accnx *dt
x =x +vx *dt
#w.g3 "set "; int( 10 +t /2.5e3 *360); " "; int( 10 +( R +5 *x))
scan
next t
#w.g1 "flush"
wait
sub turn angle ' increment/update global turtle direction ( in DEGREES)
Ttheta =( Ttheta +angle) 'mod 360
end sub
sub forward s
dx =s *cosRad( Ttheta)
dy =s *sinRad( Ttheta)
TX =TX +dx
TY =TY +dy
end sub
function sgn( j)
if j <0 then sgn =-1 else sgn =1
end function
function sinRad( a)
sinRad =sin( a *pi /180)
end function
function cosRad( a)
cosRad =cos( a *pi /180)
end function
function co$( I)
r =int( 128 +127 *sin( I / 330000))
g =int( 128 +127 *sin( I / 170000))
b =int( 128 +127 *sin( I / 070000))
co$ =str$( r) +" " +str$( g) +" " +str$( b)
end function
sub quit h$
close #h$
end
end sub